Integrate Smoothing Kernels.

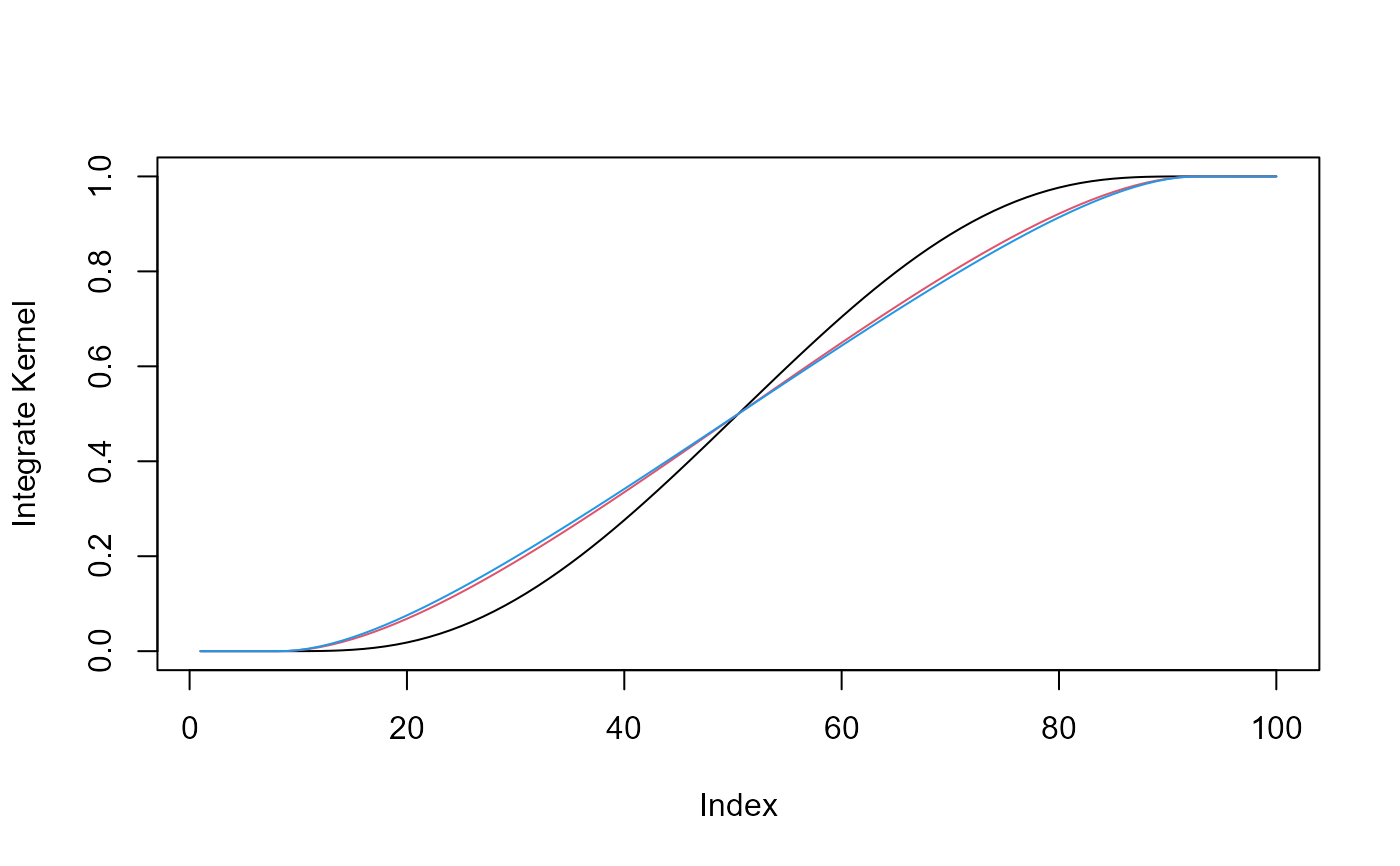
Represent integrate kernels: normal, cosine, triweight, quartic and uniform.

Usage

Kernel.integrate(u, Ker = Ker.norm, a = -1)

Arguments

u: data
Ker: Type of Kernel. By default normal kernel.
a: Lower limit of integration.

Value

Returns integrate kernel.

Details

Type of integrate kernel:

	Integrate Normal Kernel: `IKer.norm`
	Integrate Cosine Kernel: `IKer.cos`
	Integrate Epanechnikov Kernel: `IKer.epa`
	Integrate Triweight Kernel: `IKer.tri`
	Integrate Quartic Kernel: `IKer.quar`
	Integrate Uniform Kernel: `IKer.unif`

References

Ferraty, F. and Vieu, P. (2006). Nonparametric functional data analysis. Springer Series in Statistics, New York.

Hardle, W. Applied Nonparametric Regression. Cambridge University Press, 1994.

Author

Manuel Febrero-Bande, Manuel Oviedo de la Fuente manuel.oviedo@udc.es

Examples

y=qnorm(seq(.1,.9,len=100))
d=IKer.tri(y)
e=IKer.cos(y)
e2=Kernel.integrate(u=y,Ker=Ker.cos)
e-e2
#>   [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#>  [38] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#>  [75] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
f=IKer.epa(y)
f2=Kernel.integrate(u=y,Ker=Ker.epa)
f-f2
#>   [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#>  [38] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#>  [75] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
plot(d,type="l",ylab="Integrate Kernel")
lines(e,col=2,type="l")
lines(f,col=4,type="l")